728x90
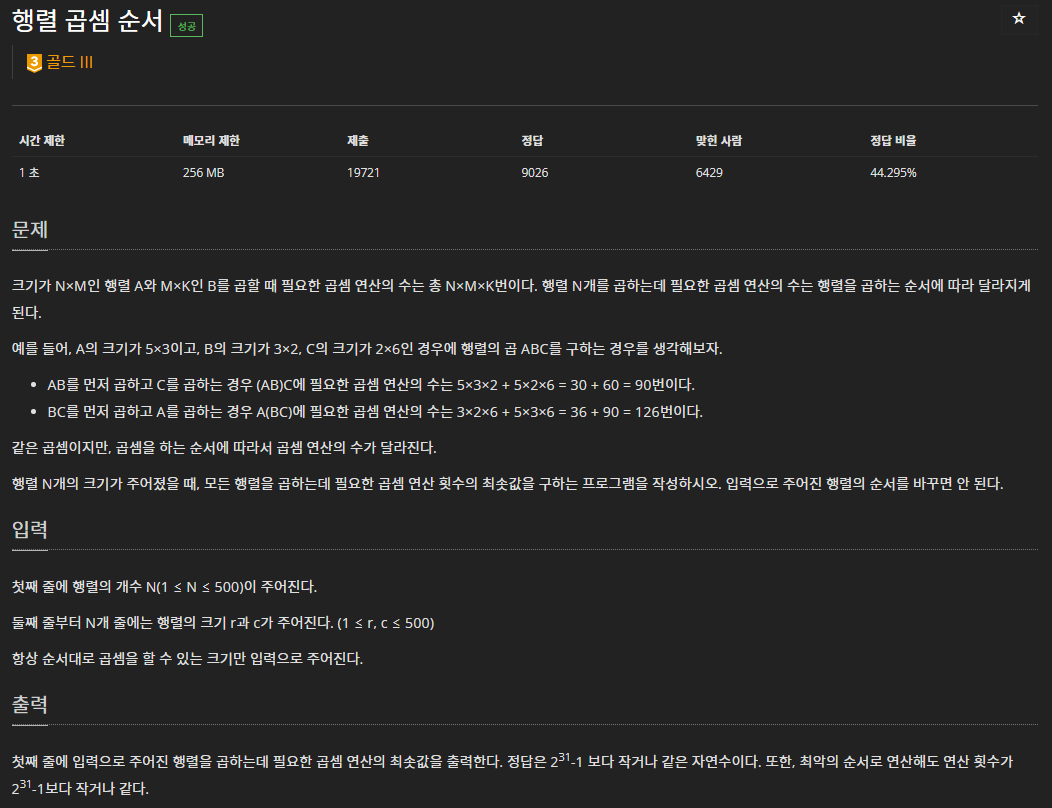

해당 문제는 거진 3일? 4일? 생각했다가 파일합치기를 응용하면 된다는 것은 알지만 점화식이 도출안돼서 답답해하다가 범죄도시 2 영화 보고 카페와서 깨닫고 풀 수 있게 된 문제이다.
파일합치기에서 응용이므로 참고하면 좋을 것 같다.
2022.05.08 - [알고리즘공부(AlgorithmStudy)/문제풀이(ProblemSolving)] - 백준 11066 java - 파일합치기(DP)
백준 11066 java - 파일합치기(DP)
해당 문제의 경우 1주일 정도 붙잡고 있다가 결국 구선생님의 도움으로 풀게 된 문제이다. 아이디어 자체는 생각할 수 있었는데 그게 맞는 건지, 구현을 어떻게 해야하는 지 감이 오질 않았다. dp
chaaany.tistory.com
<문제 풀이/접근과정>
1. 두 개의 파일을 합칠 때 필요한 비용 = 두 파일 크기의 합
2. 최종행렬 만드는 데 합치는 횟수 = 총 행렬 -1
3. 행렬의 곱 특성상 서로 인접한 파일들끼리만 합칠 수 있음
4. 점화식 도출 - f(i, j) = min(f(i, j), f(i, k-1) + f(k, j) + arr[i][0]*arr[k-1][1] * arr[j][1])
<소스코드>
package boj;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Boj_11049 {
public static void main(String[] args) throws NumberFormatException, IOException {
// 점화식 도출
// f(i, j) = min(f(i,j), f(i, k) + f(k, j))
// 곱하는 식 a, b / b, c / c, d / d, e
// 1, 2 = a * b * c
//
// 1, 3 = min(a * b * c + a * c * d, b * c * d + a * b * d)
// = min(arr[1][0] * arr[1][1] * arr[2][1] + arr[1][0] * arr[2][1] *arr[3][1]
// f(i, j) = min(f(i, j), f(i, k-1) + f(k, j) + arr[i][0]*arr[k-1][1] * arr[j][1])
// 1, 4 = 1,2 / 1, 3 / 1, 4
// = 2, 3 / 1, 3 / 1, 4
// = 2, 3 / 2, 4 / 1, 4
// = 3, 4 / 2, 4 / 1, 4
// = 1, 2, / 3, 4 / 1, 4
// f(i, j) = min(f(i, j), f(i, k) + f(k, j))
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stz;
StringBuilder sb = new StringBuilder();
int n = Integer.parseInt(br.readLine());
int arr[][] = new int[n + 1][2];
int dp[][] = new int[n + 1][n + 1];
for (int j = 1; j <= n; j++) {
stz = new StringTokenizer(br.readLine());
arr[j][0] = Integer.parseInt(stz.nextToken());
arr[j][1] = Integer.parseInt(stz.nextToken());
}
for (int end = 2; end <= n; end++) { // 도착
for (int start = end - 1; start > 0; start--) { // 출발
dp[start][end] = Integer.MAX_VALUE; // dp배열 초기화
for (int pass = start; pass < end; pass++) { // 경유
dp[start][end] = Math.min(dp[start][end], dp[start][pass] + dp[pass + 1][end] + arr[start][0] * arr[pass][1] * arr[end][1]);
}
}
}
System.out.print(dp[1][n]);
}
}728x90
'프로그래밍공부(Programming Study) > 알고리즘-문제풀이(Problem Solving)' 카테고리의 다른 글
| 백준 24479 & 24480 알고리즘 수업 - 깊이 우선 탐색 1&2(DFS) (0) | 2022.05.24 |
|---|---|
| 백준 1520 java - 내리막길(DP, 동적계획법) (0) | 2022.05.23 |
| 백준 1358 java - 하키(기하/백준단계별로풀기 기하 clear) (0) | 2022.05.19 |
| 백준 1004 java - 어린왕자(기하) (0) | 2022.05.18 |
| 백준 2477 java - 참외밭(기하) (0) | 2022.05.18 |


댓글