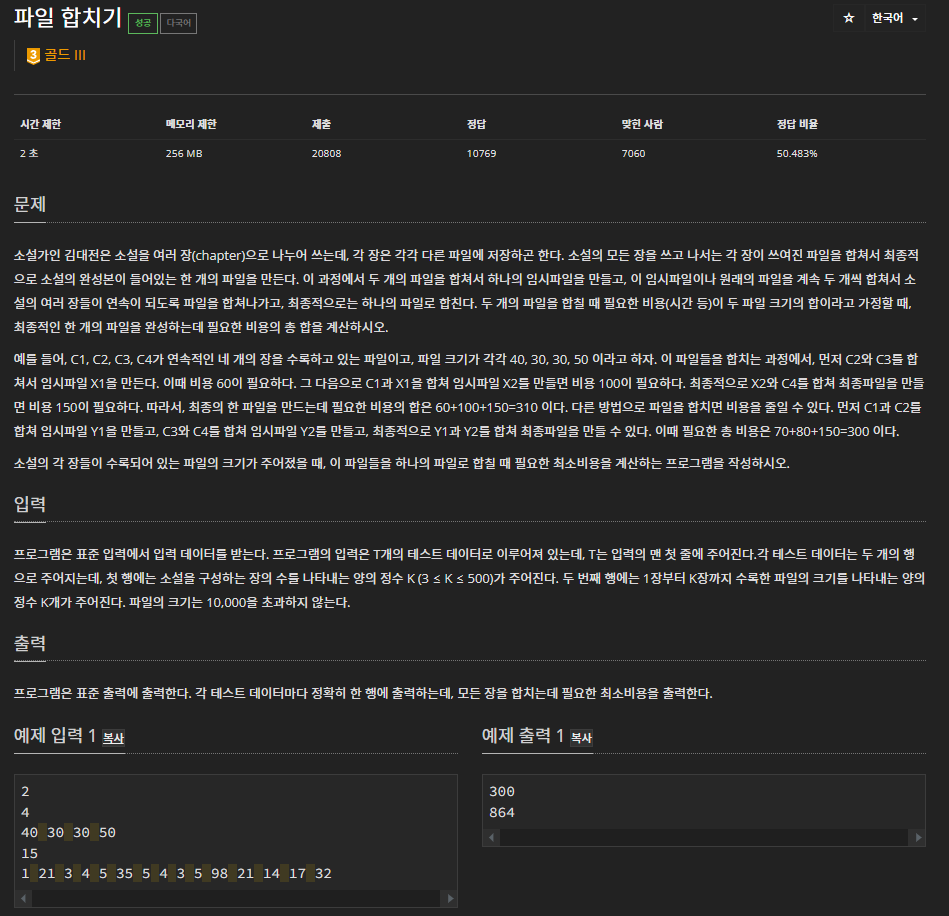
해당 문제의 경우 1주일 정도 붙잡고 있다가 결국 구선생님의 도움으로 풀게 된 문제이다.
아이디어 자체는 생각할 수 있었는데 그게 맞는 건지, 구현을 어떻게 해야하는 지 감이 오질 않았다.
dp의 세계는 정말 무궁무진한 것 같다.
<문제 접근/풀이과정>
1. 두 개의 파일을 합칠 때 필요한 비용 = 두 파일 크기의 합
2. 최종파일 만드는 데 합치는 횟수 = 총 파일 -1
3. 서로 인접한 파일들끼리만 합칠 수 있음
4. 테스트케이스 관찰 결과
C1 + C2 / C1 + C2 + C3 / C1 + C2 + C3 + C4 = 3*C1 + 3*C2 + 2*C3 + C4 = 9 / 3 3 2 1
C1 + C2 / C3 + C4 / C1 + C2 + C3 + C4 = 2*(C1 + C2 + C3 + C4) = 8 = 2 2 2 2
C2 + C3 / C1 + C2 + C3 / C1 + C2 + C3 + C4 = 2*C1 + 3*C2 + 3*C3 + C4 = 9 / 2 3 3 1
C2 + C3 / C2 + C3 + C4 / C1 + C2 + C3 + C4 = C1 + 3*C2 + 3*C3 + 2*C4 = 9 / 1 3 3 2
C3 + C4 / C2 + C3 + C4 / C1 + C2 + C3 + C4 = C1 + 2*C2 + 3*C3 + 3*C4 = 9 / 1 2 3 3
-> 결국 각각 분할해서 보면서 전체 합치기 전(sum-C1~C4)까지의 전까지 분할된 값들의 합이 적은 경우가 답일 수밖에 없다.
5. 특정 구간의 총합을 구하기 위해 고등학교 수열 시간에 배운 시그마 - 시그마 = 특정 구간의 합이라는 공식을 활용해야 함 (sum[n ~m] = sum[m] - sum[n-1])
6. dp 점화식은 다음과 같다
start 부터 end 까지의 최소비용 =
(start부터 pass까지의 최소비용 + (pass+1)부터 end까지의 최소비용 + start부터 end구간까지의 총합)의 최소비용
dp[start][end] = min(dp[start][end], dp[start][pass] + dp[pass+1][end] + sum[end]-sum[start-1])
7. sum[end]-sum[start-1]의 값은 dp구한다음에 합해줘도 상관 없긴 하다.

804ms(소스코드 ver1) => dp[start][end] = min(dp[start][end], dp[start][pass] + dp[pass+1][end] + sum[end]-sum[start-1]) 점화식으로 푼 것
956ms(소스코드 ver2) => dp[start][end] = min(dp[start][end], dp[start][pass] + dp[pass+1][end])로 dp 배열 구한 후 sum값을 나중에 더해줌
<804ms(소스코드 ver1) >
=> dp[start][end] = min(dp[start][end], dp[start][pass] + dp[pass+1][end] + sum[end]-sum[start-1]) 점화식으로 푼 것
package boj;
import java.io.*;
import java.util.*;
public class Boj_11066 {
public static void main(String[] args) throws Exception {
// 1. 두 개의 파일을 합칠 때 필요한 비용 = 두 파일 크기의 합
// 2. 최종파일 만드는 데 합치는 횟수 = 총 파일 -1
// 3. 서로 인접한 파일들끼리만 합칠 수 있음
// 40 30 30 50 => 40 60 50 => 100 50 =>
// 40 30 30 50 => 70 30 50 => 70 80
// 40 30 30 50 => 40 30 80 => 70 80
//
//
// 40 60 50 60 60 100 150
//
// 70 30 50 =
// 40 30 80 = 80 70 150
//
// C1 + C2 / C1 + C2 + C3 / C1 + C2 + C3 + C4 = 3*C1 + 3*C2 + 2*C3 + C4 = 9 / 3 3 2 1
// C1 + C2 / C3 + C4 / C1 + C2 + C3 + C4 = 2*(C1 + C2 + C3 + C4) = 8 = 2 2 2 2
// C2 + C3 / C1 + C2 + C3 / C1 + C2 + C3 + C4 = 2*C1 + 3*C2 + 3*C3 + C4 = 9 / 2 3 3 1
// C2 + C3 / C2 + C3 + C4 / C1 + C2 + C3 + C4 = C1 + 3*C2 + 3*C3 + 2*C4 = 9 / 1 3 3 2
// C3 + C4 / C2 + C3 + C4 / C1 + C2 + C3 + C4 = C1 + 2*C2 + 3*C3 + 3*C4 = 9 / 1 2 3 3
// 4. 분할정복느낌이 물씬 풍김
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
StringTokenizer stz;
StringBuilder sb = new StringBuilder();
for (int i = 0; i < T; i++) {
int n = Integer.parseInt(br.readLine());
int arr[] = new int[n+1];
int sum[] = new int[n+1];
int dp[][] = new int[n+1][n+1]; // 0 번째와
stz = new StringTokenizer(br.readLine());
for (int j = 1; j <= n; j++) { // 배열 값과 합계값 미리 넣어 두기
arr[j] = Integer.parseInt(stz.nextToken());
sum[j] = sum[j-1] + arr[j];
}
for (int end = 2; end <= n; end++) { // 도착
for (int start = end-1; start > 0; start--) { // 출발
dp[start][end] = Integer.MAX_VALUE; // dp배열 초기화
for (int pass = start; pass < end; pass++) { // 경유
dp[start][end] = Math.min(dp[start][end], dp[start][pass] + dp[pass+1][end]+ sum[end]-sum[start-1]);
}
}
}
sb.append(dp[1][n]).append("\n");
}
sb.setLength(sb.length()-1);
System.out.println(sb.toString());
}
}
<956ms(소스코드 ver2) >
=> dp[start][end] = min(dp[start][end], dp[start][pass] + dp[pass+1][end])로 dp 배열 구한 후 sum값을 나중에 더해줌
package boj;
import java.io.*;
import java.util.*;
public class Boj_11066 {
public static void main(String[] args) throws Exception {
// 1. 두 개의 파일을 합칠 때 필요한 비용 = 두 파일 크기의 합
// 2. 최종파일 만드는 데 합치는 횟수 = 총 파일 -1
// 3. 서로 인접한 파일들끼리만 합칠 수 있음
// 40 30 30 50 => 40 60 50 => 100 50 =>
// 40 30 30 50 => 70 30 50 => 70 80
// 40 30 30 50 => 40 30 80 => 70 80
//
//
// 40 60 50 60 60 100 150
//
// 70 30 50 =
// 40 30 80 = 80 70 150
//
// C1 + C2 / C1 + C2 + C3 / C1 + C2 + C3 + C4 = 3*C1 + 3*C2 + 2*C3 + C4 = 9 / 3 3 2 1
// C1 + C2 / C3 + C4 / C1 + C2 + C3 + C4 = 2*(C1 + C2 + C3 + C4) = 8 = 2 2 2 2
// C2 + C3 / C1 + C2 + C3 / C1 + C2 + C3 + C4 = 2*C1 + 3*C2 + 3*C3 + C4 = 9 / 2 3 3 1
// C2 + C3 / C2 + C3 + C4 / C1 + C2 + C3 + C4 = C1 + 3*C2 + 3*C3 + 2*C4 = 9 / 1 3 3 2
// C3 + C4 / C2 + C3 + C4 / C1 + C2 + C3 + C4 = C1 + 2*C2 + 3*C3 + 3*C4 = 9 / 1 2 3 3
// 4. 분할정복느낌이 물씬 풍김
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
StringTokenizer stz;
StringBuilder sb = new StringBuilder();
for (int i = 0; i < T; i++) {
int n = Integer.parseInt(br.readLine());
int arr[] = new int[n+1];
int sum[] = new int[n+1];
int dp[][] = new int[n+1][n+1]; // 0 번째와
stz = new StringTokenizer(br.readLine());
for (int j = 1; j <= n; j++) { // 배열 값과 합계값 미리 넣어 두기
arr[j] = Integer.parseInt(stz.nextToken());
sum[j] = sum[j-1] + arr[j];
}
for (int end = 2; end <= n; end++) { // 도착
for (int start = end-1; start > 0; start--) { // 출발
dp[start][end] = Integer.MAX_VALUE; // dp배열 초기화
for (int pass = start; pass < end; pass++) { // 경유
dp[start][end] = Math.min(dp[start][end], dp[start][pass] + dp[pass+1][end]);
}
dp[start][end] += sum[end]- sum[start-1]; // 마지막에는 싹다 더한 값이 들어감 (시그마 - 시그마로 특정 구간의 합을 구함)
}
}
sb.append(dp[1][n]).append("\n");
}
sb.setLength(sb.length()-1);
System.out.println(sb.toString());
}
}
dp[start][end] = min(dp[start][end], dp[start][pass] + dp[pass+1][end]
dp의 세계로 돌아왔으니 점화식 구하기에 전념해봐야겠다!
'프로그래밍공부(Programming Study) > 알고리즘-문제풀이(Problem Solving)' 카테고리의 다른 글
| 백준 16139 java - 인간-컴퓨터 상호작용(누적합) (0) | 2022.05.11 |
|---|---|
| 백준 2559 java - 수열(누적합) (0) | 2022.05.10 |
| 백준 13549 java - 숨바꼭질 3(BFS) (0) | 2022.05.06 |
| 백준 2470 java - 두 용액(투 포인터) (0) | 2022.05.05 |
| 백준 3273 java 두 수의 합(투 포인터) (0) | 2022.05.05 |


댓글