728x90
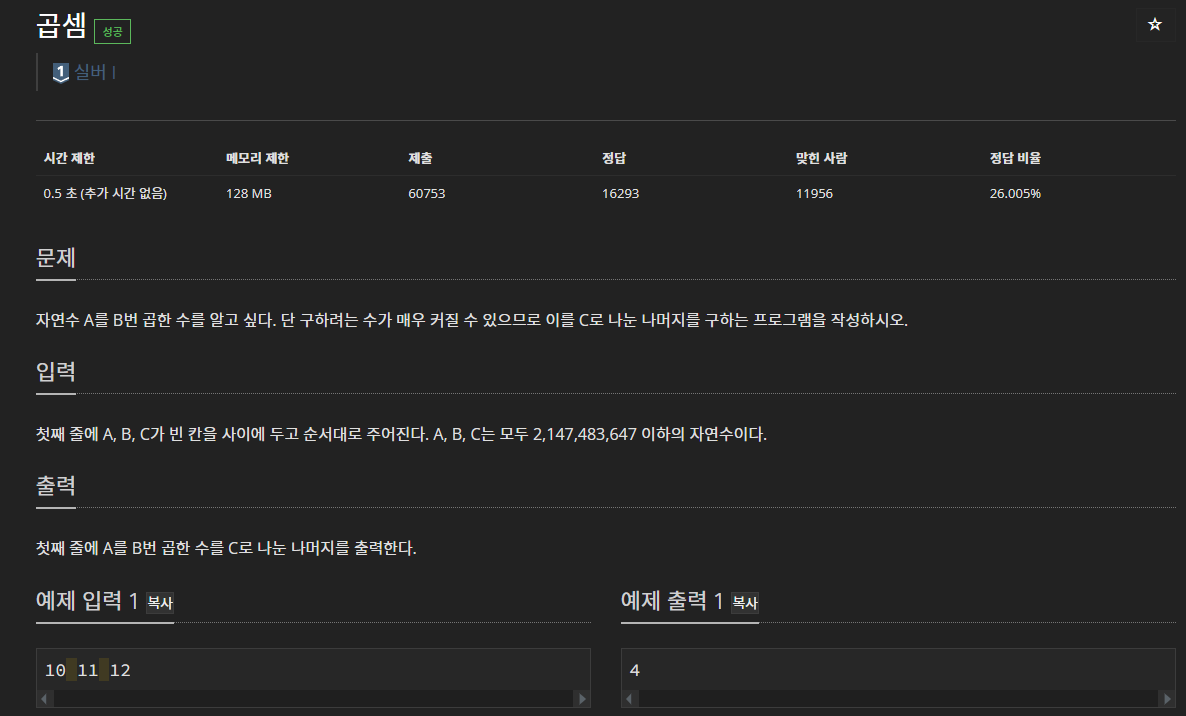
해당 문제는 쉽게 보면 쉽고 어렵게 보면 어려운 문제이다.
모듈러 연산을 활용한 것이기 때문에 모듈러의 특징을 잘 알아야 한다.
해당 문제에 대해서 두 가지의 풀이법으로 풀어보았으니 참고하시라!
<문제 풀이/접근과정>
1. 거듭제곱의 지수는 합연산이다.
ex1) x^7 = x^(1+3+3) -> x^(1+(1+1+1)+(1+1+1))
ex2) x^4 = x^(2+2) -> x^((1+1) + (1+1));
2. 지수가 0일 때 1이며, 1일 때는 자기자신 이다.
3. 결국
f(x) x는 지수
x = 1일 때 x;
x = 0일 때 1;
x가 홀수 일 때 x * (x/2) *(x/2)
x가 짝수 일 때 (x/2)*(x/2)
라는 점화식이 도출된다.
4. 모듈러 연산이란 합, 차, 곱연산에 대해서 (A 연산 B) mod C ==(동치) A mod C 연산 B mod C
참고로 모듈러 연산에 있어서 나눗셈의 경우 페르마 소정리에 의거하여 a^(p-2) = 1/a(mod p)를 활용하면 된다.
a^p = a(mod p)이므로 a를 양쪽에서 두 번 나누면 도출된다.
package boj;
import java.util.Scanner;
public class Boj_1629 {
public static void main(String[] args) {
// 11-> x * x^10 / x * x^5 * x^5
Scanner sc = new Scanner(System.in);
long A, B, C;
A = sc.nextLong();
B = sc.nextLong();
C = sc.nextLong();
long answer = power(A, B, C);
System.out.println(answer);
}
// f(x)
// x = 1일 때 x;
// x = 0일 때 1;
// x가 홀수 일 때 x * (x/2) *(x/2)
// x가 짝수 일 때 (x/2)*(x/2)
// 101 -> 1 x 50 x 50
// 50 -> 25 x 25
// 25 -> 1 x 12 x 12
// 12 -> 6 x 6
// 6 -> 3 x 3
// 3 -> 1 x 1x 1
// 1 -> 1
// x / x * x / x*x*x*x / x*x*x*x*x*x*x*x
// 7 3 1
// while문 버전
private static long power(long a, long y, long p) {
long x = a % p;
long answer = 1L;
while(y > 0) {
if((y & 1) == 1) {
answer = answer * x % p;
}
x = x * x % p;
y >>= 1;
}
return answer;
}
// 재귀 버전
private static long power(long a, long y, long p) {
if(y == 0) return 1;
if(y == 1) return a % p;
long temp = power(a, y/2, p);
if((y & 1) == 1) {
return a % p * temp % p * temp % p % p;
}else {
return temp % p * temp % p % p;
}
}
}
728x90
'프로그래밍공부(Programming Study) > 알고리즘-문제풀이(Problem Solving)' 카테고리의 다른 글
| 백준 7662 JAVA - 이중 우선순위 큐 (0) | 2022.04.23 |
|---|---|
| 백준 10830 java - 행렬 제곱 (2) | 2022.04.22 |
| 백준 1780 java - 종이의 개수 (0) | 2022.04.20 |
| 백준 5430 java - AC (0) | 2022.04.19 |
| 백준 1021- 회전하는 큐 JAVA (0) | 2022.04.18 |


댓글