728x90
문제 설명
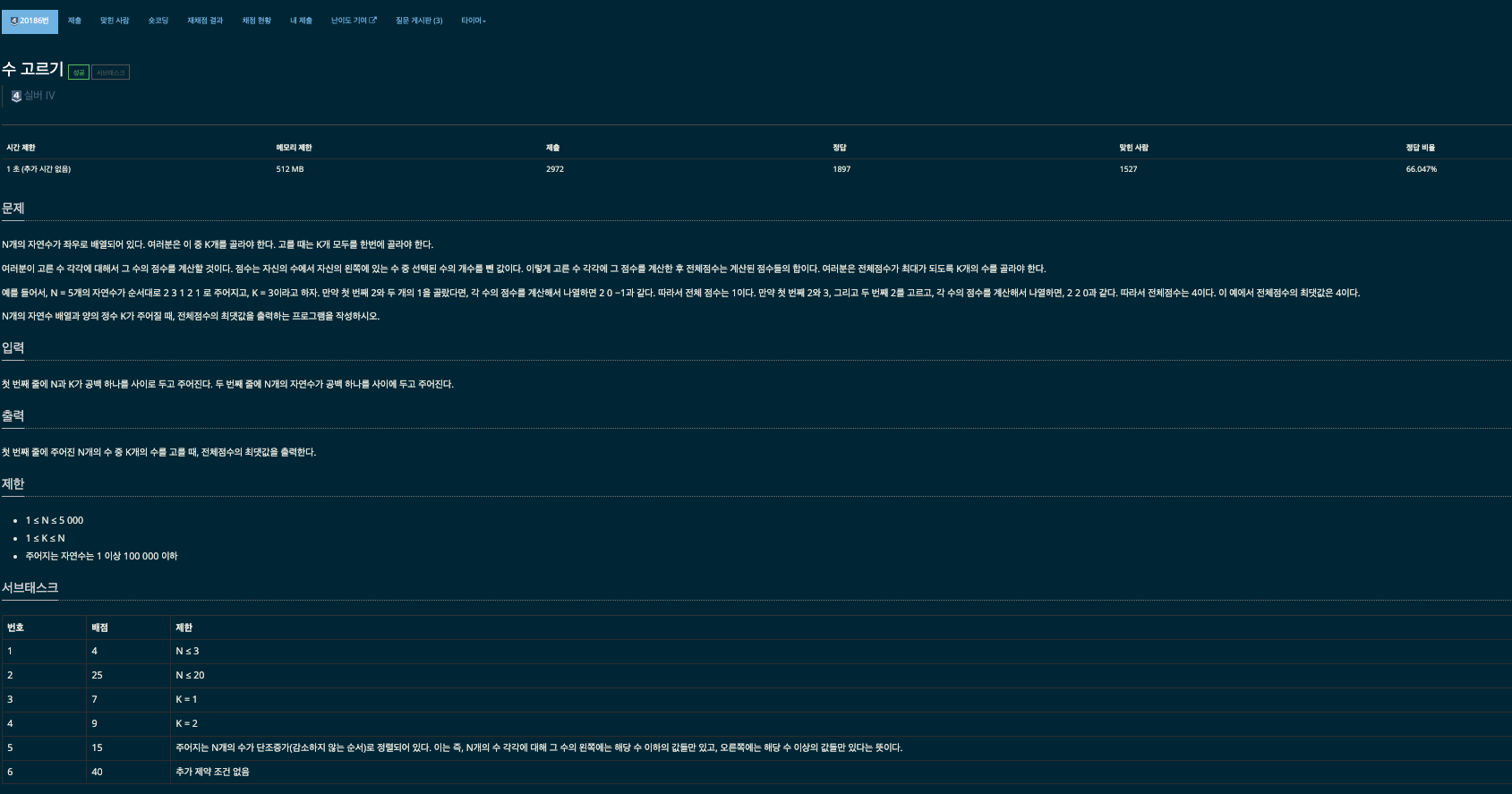
백준 20186번 "수 고르기" 문제는 주어진 수열에서 특정 개수의 수를 선택하여 최대 합을 구하는 문제입니다. 단, 선택된 숫자의 합에서 특정 공식을 활용한 감산값이 존재하므로, 이에 따라 최적화된 선택이 중요합니다.
목차
- 문제 요약 및 제약 조건
- 풀이 아이디어
- 코드 설명
- 코드 분석
- 최적화 방안
1. 문제 요약 및 제약 조건
- 입력:
- 첫 줄: (N) (수열의 길이)와 (K) (선택할 숫자의 개수).
- 둘째 줄: (N)개의 정수.
- 출력:
- (K)개의 숫자를 선택해 얻을 수 있는 최대 합.
- 감산 공식: 선택한 (K)개의 수의 합에서 (K \times (K-1) / 2)를 빼야 합니다.
2. 풀이 아이디어
- 그리디 알고리즘 활용:
- 수열을 내림차순으로 정렬.
- 가장 큰 수부터 (K)개를 선택해 합산.
- 감산 처리:
- (1, 2, 3, \ldots, (K-1))의 합인 (K \times (K-1) / 2)를 결과에서 차감.
3. 코드 설명
# 입력 처리
N, K = map(int, input().split())
number_list = list(map(int, input().split()))
# 내림차순 정렬
number_list.sort(reverse=True)
# 합산 및 감산 처리
answer = 0
for i in range(K):
answer += number_list[i]
answer -= int(K * (K - 1) / 2)
# 결과 출력
print(answer)4. 코드 분석
- 정렬:
- (O(N \log N))의 시간 복잡도를 가집니다.
- 내림차순 정렬을 통해 큰 수를 우선적으로 선택.
- 합산 및 감산:
- 루프: (K)번의 반복이므로 (O(K)).
- 감산 공식: (K \times (K-1) / 2)는 상수 시간에 계산.
- 최종 시간 복잡도:
- 전체 시간 복잡도는 (O(N \log N + K)).
5. 최적화 방안
- 정렬 최적화:
- Python의
heapq를 사용해 최대 (K)개의 큰 수만 유지하도록 설계하면 정렬 비용을 감소시킬 수 있습니다. - 시간 복잡도 개선: (O(N \log K))로 가능.
- Python의
- 메모리 최적화:
- 큰 수 (K)개만 저장하면 되므로 메모리 사용량이 감소.
최적화된 코드
import heapq
# 입력 처리
N, K = map(int, input().split())
number_list = list(map(int, input().split()))
# 최대 K개의 큰 수만 유지
largest_k = heapq.nlargest(K, number_list)
# 합산 및 감산 처리
answer = sum(largest_k) - int(K * (K - 1) / 2)
# 결과 출력
print(answer)최적화 효과:
- 입력 크기가 클수록 (O(N \log K))의 성능이 (O(N \log N))보다 효율적.
결론
이 문제는 그리디 알고리즘과 수학적 공식을 활용하여 최적화를 구현하는 대표적인 사례입니다. 기본 코드와 최적화 코드 모두 효율적으로 동작하지만, 데이터 크기에 따라 정렬 비용을 줄이는 방식으로 더욱 효율적인 풀이를 적용할 수 있습니다.
728x90
'프로그래밍공부(Programming Study) > 알고리즘-문제풀이(Problem Solving)' 카테고리의 다른 글
| 백준 19644번: 좀비 떼가 기관총 진지에도 오다니 문제풀이 (0) | 2024.12.07 |
|---|---|
| 백준 1059번: 좋은 구간 문제 풀이 (1) | 2024.12.05 |
| 백준 20044번: Project Teams 문제 풀이 (0) | 2024.12.04 |
| 백준 28353번: 고양이 카페 문제 풀이 (2) | 2024.12.04 |
| [순열 사이클 분할] 백준 10451 순열 사이클 (0) | 2024.08.10 |


댓글