728x90
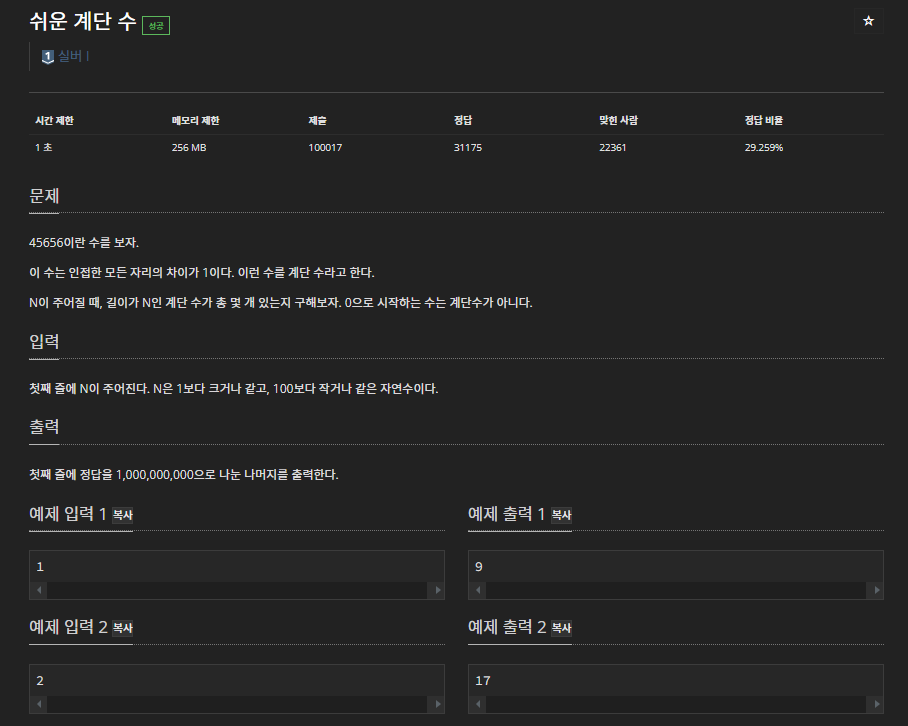
해당 문제는 실버 1이었지만 단계별로 풀이 문제 중에 실버2, 3문제랑 비교해봤을 때 상대적으로 쉬웠던 문제로 보인다.
티어는 그저 거들뿐 .. !! 아닌가? DP + Padding + 모듈러연산을 사용한 것이니 응용버전인 것으로 보이긴 한다...
잡담은 그만하고
DP + Padding(딱 맞는 크기의 배열을 선언하기 보다 적절히 빈 배열을 만들어서 활용하는 기법)+ 모듈러 연산을 통해서 문제를 풀었다.
문제 푸는데 소요시간 : 대략 50분
문제 접근/풀이 과정
1. 계단 수란 인접한 모든 자리의 차이가 1인 경우
2. n번 째 m으로 시작하는 수의 경우의 수 = n-1번째 m-1로 시작하는 수의 경우의 수 or n-1번째 m+1로 시작하는 수의 경우의 수
3. 추가적으로 고려해야할 부분 = 맨 앞의 수가 0인 경우는 될 수 없음 && 맨앞의 수가 9인 경우에는 이전 수가 8인 경우밖에 없음
4. 그렇다면 일단 맨 앞자리가 0인 경우 부터 9인 경우를 다 찾고 n번 째의 수가 0이 아닌 경우를 다 더하면 되지 않을까?
5. 굳이 예외케이스를 고려해야 할까? 그냥 0번째 인덱스 = 0 넣어두고 1번째 인덱스를 0으로 보고 ... 10번째인덱스를 9로 본다음 11번째 인덱스에 0으로 패딩(채워넣으면)하면 점화식으로 구해지지 않을까?
6. 답은 패딩+dp로 채워둔 배열 dp[n][1]~에dp[n][9]값을 다 더 해주면 된다!
7. 답을 10억(1000000000)으로 나눈 나머지로 출력하여야 하므로 유클리드 호제법을 사용하여 출력한다.
8. 참고) 모듈러연산을 자세히 설명하기 보다 공식만 보여드립니다.
다음 식은 모듈로 합동의 동치이다. (기호 ≡ 로 표시)(출처 :https://gamedevlog.tistory.com/44)
A ≡ B (mod C)
A mod C = B mod C
A = B + K * C (K는 정수) <=> A - B = K * C
코드는 바텀업 방식으로 DP를 구현하였습니다.
package boj;
import java.util.Scanner;
public class Boj_10844 {
public static void main(String[] args) {
// 계단 수 => 인접한 모든 자리의 차이가 1
// n번째 수 = n-1번째 수 +1 or n-1 번째 수 -1;
// n-1번째가 0인 경우 = dp[n-2][1];
// dp[n][1] = dp[n-1][0] + dp[n-1][2];
// dp[n][9] = dp[n-1][8];
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// 0번 인덱스 = 안씀, 1번인덱스 = 0, ... 10번인덱스 = 9, 11번 인덱스 = 안씀(0)
long dp[][] = new long[n+1][12];
long answer = 0;
for (int i = 1; i <= 10; i++) {
dp[1][i] = 1;
}
for (int N = 2; N <= n; N++) {
for (int i = 1; i <= 10; i++) {
dp[N][i] = (dp[N - 1][i - 1]% 1000000000 + dp[N - 1][i + 1] % 1000000000) %1000000000;
}
}
for (int i = 1; i <= 9; i++) {
answer = (answer%1000000000 + dp[n][i]%1000000000) % 1000000000;
}
System.out.println(answer);
}
}
728x90
'프로그래밍공부(Programming Study) > 알고리즘-문제풀이(Problem Solving)' 카테고리의 다른 글
| 백준 11053 - 가장 긴 증가하는 부분 수열 JAV (0) | 2022.03.31 |
|---|---|
| 백준 2156 - 포도주 시식 JAVA (0) | 2022.03.29 |
| 백준 2579 - 계단 오르기 JAVA (2) | 2022.03.27 |
| 백준 1932 - 정수 삼각형 JAVA (0) | 2022.03.26 |
| 백준 9251 - LCS JAVA (0) | 2022.03.24 |


댓글